Подпокрытие — это… Что такое Подпокрытие?
Лемма Гейне — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Лемма Гейне — Бореля — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Теорема Александера о предбазе — Теорема Александера о предбазе[1] (англ. Alexander Subbase Theorem) теорема общей топологии, устанавливающая критерий компактности топологического пространства. Компактным называется пространство, допускающая выделение из каждого своего… … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X.
Глоссарий общей топологии — Эта страница глоссарий. См. также основную статью: Общая топология В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глос … Википедия
БИКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в каждом открытом покрытии к рого содержится конечное подпокрытие того же пространства. Следующие утверждения равносильны: 1) пространство Xбикомпактно; 2) пересечение любой центрированной системы замкнутых в… … Математическая энциклопедия
БОРЕЛЯ — ЛЕБЕГА ТЕОРЕМА — о покрытии: пусть А ограниченнее замкнутое множество в Rn и G его открытое покрытие, т;, е: еистема открытых множеств, объединение к рых включает А; тогда существует конечная подсистема множеств , из G(подпокрытие), также являющаяся покрытием А … Математическая энциклопедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном.
Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
Словарь терминов общей топологии — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч … Википедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Открытое покрытие — множество — Большая Энциклопедия Нефти и Газа, статья, страница 1
Открытое покрытие — множество
Cтраница 1
Открытое покрытие множества Е называется конечным, если оно состоит из конечного числа множеств.
[1]
Окрестности Ux образуют открытое покрытие множества К. [2]
Если U — открытое покрытие множества Л в X, то st ( Л, ) — открытое подмножество пространства X, которое по предположению паракомпактно. [3]
С га), образуют
В силу непрерывности функции прообраз каждого открытого покрытия множества значений есть открытое покрытие компактной области; это последнее содержит конечное подпокрытие, которое является прообразом конечного подпокрытия множества значений. Таким образом, множество значений обладает свойством Гейне — Бореля, а это доказывает утверждение. [5]
Иначе говоря, система (31.9) называется открытым покрытием множества Е, если каждая точка этого множества принадлежит хотя бы одному множеству Ga из системы И.
Подмножество К метрического пространства X называется компактным, если каждое открытое покрытие множества К содержит конечное подпокрытие. [7]
Доказать, что метрическое пространство ( X, d) сепарабельно тогда и только тогда, когда каждое открытое покрытие множества X содержит счетное подпокрытие. [8]
Для того чтобы множество Л в отделимом топологическом пространстве Е было компактно, необходимо и достаточно, чтобы всякое открытое покрытие множества
I семейство, обравованное всеми В у которых К i, и всеми А, у которых Я — i, было открытым покрытием множества F. At, у которых i f, образуют покрытие множества F. [10]
Заметим, что первое условие равносильно требованию, чтобы JA не равнялась нулю тождественно.
C образует открытое покрытие множества С.
[11]
Отображение ( К, а, 6) н — — Ал ( 1 — К) Ь произведения IxAxB в Е непрерывно, и поэтому его образ D компактен. Действительно, пусть ( Ог -) образуют
Допустим, что F сг К а X, множество F замкнуто ( относительно X), а К — компактно. Если присоединить множество Р к Va, то мы получим открытое покрытие Q множества
Страницы: 1
Покрытие множества
Покрытие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами.
Пусть дано множество X {\displaystyle X}. Семейство множеств C = { U α } α ∈ A {\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X {\displaystyle X}, если
X ⊆ ⋃ α ∈ A U α. {\displaystyle X\subseteq \bigcup \limits _{\alpha \in A}U_{\alpha }.}
Пусть дано топологическое пространство X, T {\displaystyle X,{\mathcal {T}}}, где X {\displaystyle X} — произвольное множество, а T {\displaystyle {\mathcal {T}}} — определённая на X {\displaystyle X} топология. Тогда семейство открытых множеств C = { U α } α ∈ A ⊆ T {\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subseteq {\mathcal {T}}} называется открытым покрытием множества Y ⊆ X {\displaystyle Y\subseteq X}, если
{\displaystyle Y\subseteq \bigcup \limits _{\alpha \in A}U_{\alpha }.}
2. Связанные определения
Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие вписано во второе. Более точно, покрытие D = { V β } β ∈ B {\displaystyle D=\{V_{\beta }\}_{\beta \in B}} вписано в покрытие C = { U α } α ∈ A {\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}}, если
∀ β ∈ B ∃ α ∈ A {\displaystyle \forall \beta \in B\;\exists \alpha \in A} такое, что V β ⊆ U α. {\displaystyle V_{\beta }\subseteq U_{\alpha }.}
Покрытие C = { U α } α ∈ A {\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y {\displaystyle Y} называется фундаментальным, если всякое множество, пересечение которого с каждым множеством U ∈ C {\displaystyle U\in C} открыто в U {\displaystyle U}, открыто и в Y {\displaystyle Y}.
Покрытие C = { U α } α ∈ A {\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y {\displaystyle Y} называется локально конечным, если для каждой точки y ∈ Y {\displaystyle y\in Y} существует окрестность U ∋ y {\displaystyle U\ni y}, пересекающаяся лишь с конечным числом элементов C {\displaystyle C}, то есть множество { α ∈ A ∣ U α ∩ U ≠ ∅ } {\displaystyle \{\alpha \in A\mid U_{\alpha }\cap U\not =\varnothing \}} конечно.
Y {\displaystyle Y} называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
Y {\displaystyle Y} называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Дата публикации:
05-16-2020
Дата последнего обновления:
05-16-2020Алгоритм поиска наименьшего по мощности покрытия конечного множества его подмножествами
Разбирая старые бумаги наткнулся на изрядно потрёпанную тетрадь, в которой обнаружил наброски алгоритма поиска покрытия.
Автор алгоритма Виктор Анатольевич Щербанов — мой учитель, под руководством которого я работал в девяностые годы прошлого столетия. Моё скромное участие в основном заключалось в том, что я предлагал в большинстве случаев неверные (а порой и просто бредовые) варианты. Что в общем-то не помешало Шефу (так мы его называли между собой) таки довести работу над алгоритмом до логического завершения. Где-то в двухтысячных годах алгоритм был опубликован в одном из институтских изданий Томска. Но думаю, что не лишним будет вспомнить его ещё раз. Собственно в память о Шефе я и решил написать этот пост. Может быть алгоритм покажется кому-то интересным или подтолкнёт на какие-то новые идеи по реализации алгоритма.Сам алгоритм зиждется на двух утверждениях и двух теоремах, доказательства которых здесь не приводятся, из-за их довольно большого объёма.
Для начала определимся с тем, что мы, собственно, ищем.
Пусть задано конечное множество и семейство его подмножеств .
Найти подсемейство (если оно существует) такое, что и мощность подсемейства S* (покрытия множества V) наименьшая из всех возможных.
Следующие утверждения определяют понятия минимального и наименьшего покрытия.
Утверждение 1.
Для того чтобы подсемейство , было покрытием множества , необходимо и достаточно, чтобы выполнялось условие
Покрытие S’ называется минимальным, если не существует покрытия S» такого, что .
Покрытие S* называется наименьшим, если для любого минимального покрытия S’ выполняется условие
Утверждение 2.
Покрытие минимально тогда и только тогда, когда для любого , выполняется условие
И, самое основное.
Пусть задано конечное множество и семейство его подмножеств .
Построим полный нагруженный граф , в котором множеству вершин графа взаимно однозначно сопоставлено семейство подмножеств ,
а каждому ребру — подмножество .
Обозначим множество всех рёбер инцидентных вершине , а — множество всех вершин, инцидентных рёбрам из множества .
Теорема 1.
Минимальное по мощности подмножество ребер, инцидентных произвольной вершине в графе G, при выполнении условий
определяет минимальное покрытие , однозначно соответствующее множеству вершин, если , или множеству вершин, если .
Теорема 2.
Минимальное по мощности подмножество ребер, инцидентных произвольной вершине ребра в графе G, при выполнении условий
для всех
определяет наименьшее покрытие , однозначно соответствующее множеству вершин, если , или множеству вершин, если .
На основании теорем предлагается следующий алгоритм поиска наименьшего покрытия.
1. Множеству и семейству его подмножеств , сопоставить семейство подмножеств . Если для некоторого окажется , то существует тривиальное покрытие . Конец алгоритма.
Иначе перейти на п.2.
2. Построить полный нагруженный граф , где .
Вершину нагрузить множеством
Ребро нагрузить множеством .
3. Проверить существование покрытия: для произвольной вершины определить подмножество
,
где — множество рёбер, инцидентных вершине в графе .
Если , то покрытия не существует. Конец алгоритма.
Если , то покрытие существует.
Перейти к процедуре поиска наименьшего покрытия (п. 4).
4. Положить t:=0.
5. В полном нагруженном графе найти ребро для которого выполняется условие .
Если , то перейти на п. 6,
иначе — на процедуру построения множества D вершин, определяющих наименьшее покрытие (п. 7).
6. Построить полный нагруженный граф , полагая , — множество рёбер, инцидентных вершине в графе .
Положить для всех .
Положить t:=t+1 и перейти на п. 5.
7. Начало построения множества D вершин, определяющих наименьшее покрытие .
Положить .
8. Если t=0, то перейти на п. 11, иначе — положить t:=t-1.
9. В графе определить подмножество
10. Если в графе выполняется условие , то положить , иначе — D:=D. Перейти на п. 8.
11. Семейство подмножеств определяет наименьшее покрытие множеств .
Конец алгоритма.
Попробуем оценить сложность алгоритма.
Вся, так сказать, суть алгоритма (с точки зрения оценки сложности) заключена в фразе «построим полный нагруженный граф».
Нам требуется выполнить n действий для вычисления нагрузки в n вершинах графа и (n-1)n/2 вычислений (по количеству рёбер полного графа) для нагрузки рёбер графа. И всё это, если рассматривать наихудший случай, когда подмножества взаимно не пересекаются, выполняется n-2 раза. Таким образом грубая оценка O(n) = n3 + n2.
И в заключение. Не уверен, что пост заслуживает инвайта, потому как моя причастность к алгоритму более чем сомнительная. Но опубликования, как мне кажется, стоит. Надеюсь модераторы разберутся.
Как там греки говорили? — Fais se que dois adviegne que peut (делай, что должно, и будь, что будет).
(или это были римляне?)
НОУ ИНТУИТ | Лекция | Элементы теории реляционных баз данных: функциональные зависимости и декомпозиция без потерь
Аннотация: Эта и две следующие лекции посвящены вопросам теории реляционных баз данных. Поскольку все направление реляционного подхода к организации баз данных является сугубо практическим, эта теория, главным образом, прагматическая.
Основная проблема, на решение которой направлена теория реляционных баз данных, состоит в обнаружении полезных свойств некоторых схем баз данных и выработке способов построения таких схем. Принято кратко называть эту проблему проблемой проектирования реляционных баз данных.
Введение
Несмотря на свою практическую ориентированность, теория реляционных баз данных является самостоятельным научным направлением, в котором работали (и продолжают работать) многие известные исследователи, чьи имена будут встречаться в наших лекциях. Мы не планировали в данном курсе подробно описывать основные результаты в области теории реляционных баз данных. Наша цель состоит в том, чтобы обеспечить только определения и утверждения, необходимые для общего понимания процесса проектирования реляционных баз данных на основе нормализации.
Поскольку наиболее важные с практической точки зрения свойства реляционных баз данных базируются на понятии функциональной зависимости, мы выделили в отдельную лекцию краткое обсуждение соответствующих теоретических вопросов.
Среди этих вопросов наибольший интерес представляют замыкания и покрытия множеств функциональных зависимостей, аксиомы Армстронга и теорема Хита о достаточном условии декомпозиции отношения без потерь. Понятия и утверждения данной лекции действительно нужны для усвоения материала лекции 7, но мы стремились еще и продемонстрировать читателям на несложных примерах, что собой представляет теория реляционных
баз данных, каков уровень ее сложности и насколько она понятна интуитивно.
Заметим, что мы не выделяли в отдельные лекции теоретический материал, касающийся многозначных зависимостей и зависимостей соединения. Это было сделано по двум причинам. Во-первых, эти виды зависимостей реже встречаются при моделировании предметной области средствами баз данных. Поэтому мы сочли достаточным представить внутри лекции 8 только основы соответствующего теоретического материала. Во-вторых, хотя теория многозначных зависимостей и зависимостей соединения, по сути, не намного сложнее теории функциональных зависимостей, ее определения и утверждения слишком громоздки для данного курса.
Функциональные зависимости
Наиболее важные с практической точки зрения нормальные формы отношений основываются на фундаментальном в теории реляционных баз данных понятии функциональной зависимости. Для дальнейшего изложения нам потребуется несколько определений и утверждений (по ходу изложения мы будем пояснять их и иллюстрировать).
Общие определения
Пусть задана переменная отношения r, и X и Y являются произвольными подмножествами заголовка r («составными» атрибутами).
В значении переменной отношения r атрибут Y функционально зависит от атрибута X в том и только в том случае, если каждому значению X соответствует в точности одно значение Y. В этом случае говорят также, что атрибут X функционально определяет атрибут Y ( X является детерминантом ( определителем ) для Y, а Y является зависимым от X ). Будем обозначать это как r.
X->r.Y .
Для примера будем использовать отношение СЛУЖАЩИЕ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ИМЯ, СЛУ_ЗАРП, ПРО_НОМ, ПРОЕКТ_РУК} (рис. 6.1). Очевидно, что если СЛУ_НОМ является первичным ключом отношения СЛУЖАЩИЕ, то для этого отношения справедлива функциональная зависимость (Functional Dependency – FD) СЛУ_НОМ->СЛУ_ИМЯ.
На самом деле, для тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ в том виде, в котором оно показано на рис. 6.1, выполняются еще и следующие FD (1):
Рис. 6.1. Пример возможного тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ
СЛУ_НОМ->СЛУ_ИМЯ
СЛУ_НОМ->СЛУ_ЗАРП
СЛУ_НОМ->ПРО_НОМ
СЛУ_НОМ->ПРОЕКТ_РУК
{СЛУ_НОМ, СЛУ_ИМЯ}->СЛУ_ЗАРП
{СЛУ_НОМ, СЛУ_ИМЯ}->ПРО_НОМ
{СЛУ_НОМ, СЛУ_ИМЯ}->{СЛУ_ЗАРП, ПРО_НОМ}
…
ПРО_НОМ->ПРОЕКТ_РУК и т.д.Поскольку имена всех служащих различны, то выполняются и такие FD (2):
СЛУ_ИМЯ->СЛУ_НОМ СЛУ_ИМЯ->СЛУ_ЗАРП СЛУ_ИМЯ->ПРО_НОМ и т.д.
д.Более того, для примера на рис. 6.1 выполняется и FD (3):
СЛУ_ЗАРП->ПРО_НОМ
Однако заметим, что природа FD группы (1) отличается от природы FD групп (2) и (3). Логично предположить, что идентификационные номера служащих должны быть всегда различны, а у каждого проекта имеется только один руководитель. Поэтому FD группы (1) должны быть верны для любого допустимого значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ и могут рассматриваться как инварианты, или ограничения целостности этой переменной отношения.
FD группы (2) базируются на менее естественном предположении о том, что имена всех служащих различны. Это соответствует действительности для примера из рис. 6.1, но возможно, что с течением времени FD группы (2) не будут выполняться для какого-либо значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ.
intuit.ru/2010/edi»>Наконец, FD группы (3) основана на совсем неестественном предположении, что никакие двое служащих, участвующие в разных проектах, не получают одинаковую зарплату. Опять же, данное предположение верно для примера из рис. 6.1, но, скорее всего, это случайное совпадение.В дальнейшем нас будут интересовать только те функциональные зависимости, которые должны выполняться для всех возможных значений переменных отношений.
Заметим, что если атрибут A отношения r является возможным ключом, то для любого атрибута B этого отношения всегда выполняется FD A->B (в группе (1) к этим FD относятся все FD, детерминантом которых является СЛУ_НОМ ). Обратите внимание, что наличие в отношении СЛУЖАЩИЕ_ПРОЕКТЫ FD ПРО_НОМ->ПРОЕКТ_РУК приводит к некоторой избыточности этого отношения. Имя руководителя проекта является характеристикой проекта, а не служащего, но в нашем случае содержится в теле отношения столько раз, сколько служащих работает над проектом.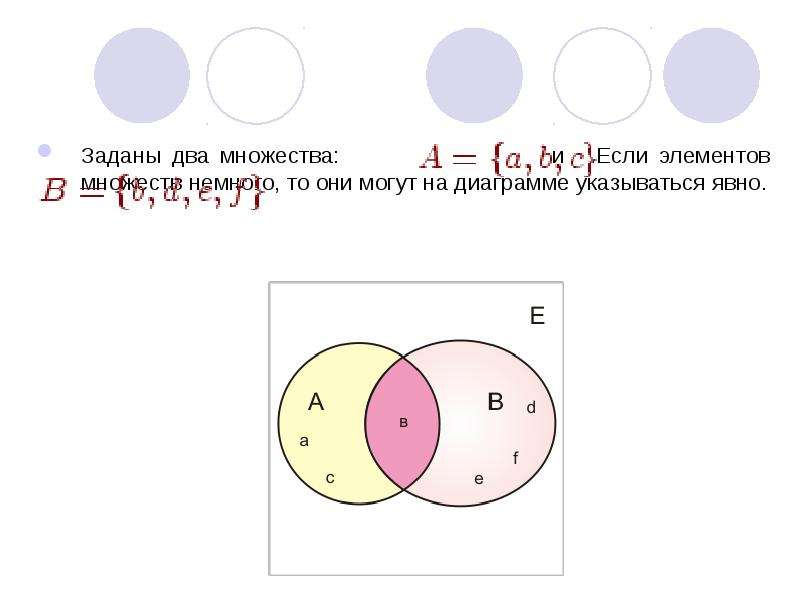
Итак, мы будем иметь дело с FD, которые выполняются для всех возможных состояний тела соответствующего отношения и могут рассматриваться как ограничения целостности. Как показывает (неполный) список (1), таких зависимостей может быть очень много. Поскольку они трактуются как ограничения целостности, за их соблюдением должна следить СУБД. Поэтому важно уметь сократить набор FD до минимума, поддержка которого гарантирует выполнение всех зависимостей. Мы займемся этим в следующих подразделах.
FD A->B называется тривиальной, если (т. е. множество атрибутов A включает множество B или совпадает с множеством B ).
Очевидно, что любая тривиальная FD всегда выполняется. Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ всегда выполняется FD {СЛУ_ЗАРП, ПРО_НОМ}->СЛУ_ЗАРП. Частным случаем тривиальной FD является A->A.
intuit.ru/2010/edi»>Поскольку тривиальные FD выполняются всегда, их нельзя трактовать как ограничения целостности, и поэтому они не представляют интереса с практической точки зрения. Однако в теоретических рассуждениях их наличие необходимо учитывать.алгоритм жадного покрытия множества — CodeRoad
Итак, я взял этот код из
Как мне ускорить реализацию жадного набора обложек?
Я пытаюсь понять наборы и установить обложку, поэтому я немного изменяю это.
U = set([1,2,3,4])
R = U
S = [set([1,2]),
set([1]),
set([1,2,3]),
set([1]),
set([3]),
set([1,2]),
set([3]),
set([1,2,3])]
w = [1, 1, 1, 1, 1, 1, 1, 1]
C = []
costs = []
def findMin(S, R):
minCost = 99999.0
minElement = -1
for i, s in enumerate(S):
try:
cost = w[i]/(len(s.intersection(R)))
if cost < minCost:
minCost = cost
minElement = i
except:
# Division by zero, ignore
pass
return S[minElement], w[minElement]
while len(R) != 0:
S_i, cost = findMin(S, R)
C. append(S_i)
R = R.difference(S_i)
costs.append(cost)
print "Cover: ", C
#print "Total Cost: ", sum(costs), costs
append(S_i)
R = R.difference(S_i)
costs.append(cost)
print "Cover: ", C
#print "Total Cost: ", sum(costs), costs
Как видно, U имеет значения 1,2,3,4. Ни в одном из наборов нет 4. Я не разбираюсь в Весах, поэтому поставил их как 1.
Ожидаемый результат: set([1,2]), set([3]) , set([1,2,3]) или что-то, что покрывает максимум доступного.
Поделиться Источник Omair . 19 сентября 2013 в 11:46
1 ответ
- Оптимальный алгоритм для решения проблемы взвешенного покрытия множества?
Извините за название, но SO не допускал в нем слова problem. У меня есть следующая проблема: У меня есть пакеты вещей, которые я хочу продать, и у каждого пакета есть цена. Когда кто-то запрашивает вещи X , Y и Z , я хочу просмотреть все пакеты, некоторые из которых содержат более одного элемента,.
.. - Алгоритм покрытия жадных множеств, построенный по *removing* множествам
Я пытаюсь реализовать решение проблемы покрытия множества с помощью жадного алгоритма. Классический алгоритм жадной аппроксимации для него таков input: collection C of sets over universe U , costs: C→R ≥0 output: set cover S 1. Let S←∅. 2. Repeat until S covers all elements: 3. Add a set s to S,…
..
1
Проблема с вашим кодом заключается в том, что нет обложки, потому что есть дополнительные 4. Насколько я понимаю, по определению проблема покрытия множеств указывает, что объединение всех множеств в S должно быть равно U . Так что лишних 4 там быть не должно.
Поскольку ваша программа не останавливается до тех пор, пока не найдет идеальное покрытие (т. Е. до тех пор, пока len(R) != 0), она никогда не остановится на этом входе.
Вы передаете неверный ввод в алгоритм.
В качестве примечания я бы настоятельно рекомендовал не использовать общее предложение except для проверки на нулевое деление. Это не очень хорошее использование try/except ; Я думаю, что это тот случай, когда вы должны посмотреть, прежде чем прыгать.
Поделиться senderle 19 сентября 2013 в 12:16
Похожие вопросы:
Алгоритм для списка всех возможных множеств множеств множества
Мне трудно придумать алгоритм для генерации списка всех возможных наборов наборов набора. Под этим я подразумеваю, что, учитывая множество S, Я хотел бы знать все возможные множества, содержащие…
Каков хороший алгоритм получения минимального вершинного покрытия дерева?
Каков хороший алгоритм получения минимального вершинного покрытия дерева? INPUT: Соседи узла. OUTPUT: Минимальное число вершин.
алгоритм поиска минимального размера покрытия набора для задачи Set-cover
В задаче покрытия множеств нам дана Вселенная U, такая, что |U / =n, а множества S1,….., Sk являются подмножествами U. Обложка набора — это коллекция C некоторых наборов из S1,….., Sk,…
Оптимальный алгоритм для решения проблемы взвешенного покрытия множества?
Извините за название, но SO не допускал в нем слова problem. У меня есть следующая проблема: У меня есть пакеты вещей, которые я хочу продать, и у каждого пакета есть цена. Когда кто-то запрашивает…
Алгоритм покрытия жадных множеств, построенный по *removing* множествам
Я пытаюсь реализовать решение проблемы покрытия множества с помощью жадного алгоритма. Классический алгоритм жадной аппроксимации для него таков input: collection C of sets over universe U , costs:…
Почему жадный алгоритм не находит максимального независимого множества двудольного графа?
Я пытался решить задачу максимального независимого множества на двудольных графах с помощью жадного метода.
Итак, я наткнулся на этот пост, который делает именно то, что я пытался сделать. Но я…
Недетерминированный алгоритм для покрытия вершин
У меня была проблема в моей классной викторине, чтобы написать недетерминированный алгоритм для покрытия вершин. Мы обсудили решение с нашим инструктором, и он сказал, что уровень неопределенности…
Нахождение минимального независимого доминирующего множества с помощью жадного алгоритма
Я разработал алгоритм, который находит минимальное независимое доминирующее множество графа на основе ограничения расстояния. (Я использовал Python и NetworkX для генерации графиков и получения пар)…
Алгоритм покрытия краевой клики
Я пытаюсь написать алгоритм, который вычисляет номер покрытия реберной клики (наименьшее число клик, покрывающих все ребра) входного графа (неориентированного и без самоциклов). Моя идея состояла бы…
Пример ввода в задачу покрытия множества, которая не обеспечивает 2-аппроксимации
Мне нужна помощь со следующим вопросом: Покажите пример входа в задачу покрытия множества, для которой жадный алгоритм, показанный в классе , не обеспечивает 2-аппроксимации.
N)$, где
$N$ — размер маски. Очевидно, что уже при 22 элементах, придётся ждать очень долго для получения всех решений.
Здесь следует отметить, что любое решение может найтись довольно быстро. Но если мы хотим убедиться, что решений нет, доказать, что оно единственное или же найти все, то время выполнения алгоритма затянется.
Рассмотрим прикладную задачу, которую я решал в своей практике.
Задача
Пусть у нас есть покупки. Мы знаем суммарную цену, т.е. общую сумму всех товаров и цену каждого товара. При этом, клиент вернул некоторые из товаров. Требуется понять, какие из товаров клиент купил.
Продолжение
В ряде случаев, нам хочется понимать, сколько решений есть у этой задачи?
Решение
Есть товары:
Каждый из них сколько-то стоит:
Также есть отправление и возврат:
Существует решение:
Включая и исключая по очереди все в решение, мы можем найти все возможные решения.
Прочитать подробнее можно тут В данном случае, используется идея о том, что не обязательно заполнять всю матрицу, а достаточно пойти от финального решения, т.е. и рекурсивно перебрать все решения. Таким образом, мы ответим на все вопросы задачи. Проблема данного подхода в том, что мы не можем делать это итеративно, а значит нам придётся все решения хранить в памяти, а их может быть довольно много.
Важно отметить, что данная задача является частным случаем задачи о рюкзаке. Задача о рюкзаке выглядит так:
Есть рюкзак, у него есть вместимость, а также мы хотим в него набрать предметов максимальной стоимости так, чтобы все они поместились. При этом, у каждого предмета есть его стоимость и вес (ограничение). Потенциально ограничений в задаче может быть более одного.
В нашем случае всё проще. Во-первых, вес рюкзака и ограничение в данном случае совпадают.
Во-вторых, в отличие от задаче о рюкзаке, нам требуется составить из наших предметов в точности максимальный вес рюкзака. Не забываем, что вес совпадает с ограничением, либо сказать, что такого решения не существует.
Для того, чтобы генерировать решения итеративно, предлагается отранжировать элементы. В данном случае это возможно, покуда ограничение и вес совпадают. Затем, на каждом шаге, мы будем набивать рюкзак, итерируясь от максимального элемента к минимальному и будем пересчитывать остаток. Как только остаток станет меньше 0, возвращемся к предыдущему шагу и продолжаем поиск. Если остаток равен в точности 0, то возвращаем решение, а затем, с того же места продолжаем поиск.
Заметим, что данное решение работает примерно в 2 раза дольше, чем решение задачи о рюкзаке. При этом, мы можем отдавать ответы итеративно.
Покрытие (набора) — Математическая энциклопедия
Любое семейство подмножеств данного множества $ X $ с объединением $ X $.
Под покрытием топологического пространства, однородного пространства или вообще любого множества, имеющего некоторую структуру, понимается любое покрытие этого множества. Однако в теории топологических пространств особенно естественно рассматривать открытые покрытия, т.е. покрытия, все элементы которых являются открытыми множествами. Значительная важность открытых покрытий возникает потому, что элементы такого покрытия содержат полную информацию о локальной структуре пространства, а свойства покрытия в целом (в частности, количество элементов, кратность и комбинаторные свойства) отражают существенные глобальные характеристики пространства.
Например, размерность Лебега dim топологического пространства определяется в терминах языка открытых покрытий: размерность нормального пространства $ X $ не превосходит натурального числа $ n $, если в каждом конечном открытом покрытии этого пространства в пространство можно вписать конечное открытое покрытие, кратность которого в каждой точке (т. е. количество элементов в покрытии, содержащем данную точку) не превышает $ n + 1 $. Отношение одного покрытия, вписанного в другое, является основным общим элементарным отношением между покрытиями.Семейство множеств $ \ gamma $ вписывается в семейство множеств $ \ lambda $, если каждый элемент семейства $ \ gamma $ содержится в некотором элементе семейства $ \ lambda $. Класс паракомпактных пространств (ср. Паракомпактное пространство) определяется в терминах открытых покрытий.
Именное подпокрытие покрытия $ \ gamma $ множества $ X $ дается любому подсемейству семейства $ \ gamma $, которое само является покрытием $ X $. Основные понятия компактности, счетной и конечной компактности определены в терминах подпокрытий.Пространство компактно, если в каждом его открытом покрытии можно указать конечное подпокрытие. Пространство счетно компактно, если в каждом его счетном открытом покрытии можно указать конечное подпокрытие. В конечном итоге пространство компактно, если в каждом его открытом покрытии можно указать счетное подпокрытие. Открытые покрытия используются для определения абстрактных комбинаторных объектов; это открыло способы применения алгебраических методов в исследовании топологических пространств, более общих, чем многогранники. P.S. Александров определил фундаментальное понятие нерва произвольного покрытия $ \ gamma $ как абстрактный комплекс, вершины которого находятся во взаимно однозначном соответствии с элементами $ \ gamma $, а конечное множество этих вершин составляет абстрактный симплекс тогда и только тогда, когда пересечение соответствующих элементов $ \ gamma $ не пусто.Системы открытых покрытий пространства вместе с отношением вписанности соответствуют системам абстрактных комплексов, связанных симплициальными отображениями, так называемым спектрам комплексов.
Закрытые покрытия также играют важную роль в топологии; это покрытия, в которых все элементы являются замкнутыми множествами. Если все одноточечные множества в топологическом пространстве замкнуты, пример замкнутого покрытия для этого пространства дается семейством всех его одноточечных подмножеств. Однако такое покрытие не содержит никакой информации о топологии пространства, за исключением того факта, что применима аксиома $ T_1 $ -разделения.Поэтому требование закрытого покрытия следует сочетать с другими существенными ограничениями. В частности, полезно рассматривать локально конечные замкнутые накрытия. Это важно в теории размерностей. Другой важный пример замкнутого покрытия — покрытие многогранника замкнутыми симплексами некоторого комплекса, разделяющего этот многогранник.
Интересные свойства покрытия связаны не с характером его элементов, а с их положением, из которых наиболее часто встречаются следующие: мощность покрытия (количество элементов в нем), локальная конечность ( для каждой точки в пространстве существует окрестность, которая пересекается с конечным числом элементов из семейства подмножеств этого пространства), точечная конечность (конечно, множество элементов покрытия, содержащего случайную точку) и звезда -подобная конечность (каждый элемент покрытия пересекается только с конечным числом элементов покрытия).
Семейство множеств в топологическом пространстве называется консервативным, если замыкание объединения любого из его подсемейств равно объединению замыканий элементов этого подсемейства. Каждое локально конечное семейство множеств консервативно. Консервативные покрытия возникают при изучении паракомпактных пространств, где любое консервативное покрытие, а не просто открывающее, важно и нетривиально.
Важную роль играет понятие звезды точки $ x $ относительно семейства множеств $ \ gamma $ (в частности, покрытия).Это объединение всех элементов в $ \ gamma $, содержащих $ x $, обычно обозначается как $ \ mathrm {St} _ {\ gamma} (x) $. Аналогично определяется звезда $ \ mathrm {St} _ {\ gamma} (A) $ множества $ A $ относительно семейства множеств $ \ gamma $. Понятие звезды используется в фундаментальном отношении, когда одно покрытие звездно вписано в другое, что значительно тоньше, чем отношение вписания. Семейство множеств $ \ lambda $ называется звездным, вписанным в семейство множеств $ \ gamma $, если для каждой точки в $ \ gamma $ найдется элемент, содержащий звезду этой точки относительно $ \ lambda $. .Отношение звездообразной вписанности для открытых покрытий важно в теории размерностей, на нем основаны некоторые критерии метризации, и это одна из основных элементарных концепций при определении однородной структуры и однородного пространства. Полезно рассмотреть семейство $ F $ открытых покрытий топологического пространства, направленное отношением звездности вписанного в следующем смысле: для любых $ \ gamma_1 $ и $ \ gamma_2 $ из $ F $ существует $ \ mu \ in F $, звездообразно вписанное как в $ \ gamma_1 $, так и в $ \ gamma_2 $.
Следующая характеристика паракомпактности на языке звездоподобного вписанного имеет важное значение (теорема Мориты): пространство Хаусдорфа паракомпактно тогда и только тогда, когда можно вписать в любое из его открытых покрытий открытое звездное покрытие.
Звездчатая надпись не имеет такого содержания для случая произвольных (или даже закрытых) покрытий. В частности, это очевидно из того факта, что семейство всех одноточечных подмножеств пространства подобно звезде вписано в любое покрытие этого пространства.
Список литературы
| [1] | Дж. Л. Келли, «Общая топология», Springer (1975) |
| [2] | A.V. Архангельский, В. Пономарев, «Основы общей топологии: задачи и упражнения», Рейдел (1984) |
Покрытие топологического пространства также называется покрытием этого пространства. Обычно в западной литературе вписанное покрытие называется уточнением, а консервативное покрытие — покрытием, сохраняющим замыкание.Далее, барицентрическое уточнение используется для звездообразного вписанного семейства (множеств). Существует также понятие звездного уточнения: семейство $ \ lambda $ множеств является звездным уточнением семейства $ \ gamma $ (множеств), если семейство $ \ {\ mathrm {St} _ {\ lambda} (A): A \ in \ lambda \} $ — это уточнение (уточнение) $ \ gamma $. Наконец, теорема Мориты широко известна как теорема Стоуна о совпадениях, доказанная А.Х. Стоуном [a1].
Список литературы
| [a1] | A.H. Stone, «Паракомпактность и пространства продуктов» Bull.n $, пусть $ \ mathrm {bd} \ K $ и $ \ mathrm {int} \ K $ — соответственно граница и внутренность $ K $. n \ backslash \ mathrm {int} \ K $, которым можно покрыть $ K $. Если $ K $ ограничен, задачи a) и b) эквивалентны, и они эквивалентны проблеме освещения (извне) для множества $ \ mathrm {bd} \ K $ и связаны с гипотезой Хадвигера. . Для неограниченного $ K $ задачи a) и b) в общем случае различны, а числа $ b (K) $ и $ t (K) $ могут быть бесконечными. Список литературы
P.S. Солтан Как цитировать эту запись: общая топология — О покрытиях, внутренних покрытиях и компактности«Если в наборе есть конечное открытое подпокрытие, то оно компактно.« Это неверно. Правильное определение: «Если каждое открытое покрытие набора имеет конечное подпокрытие, то набор компактный». «(−1,0) ∪ (−1 / 2,2) — конечное открытое покрытие (0,1)» Верно, ну и что? это не только открытая крышка (0,1) $. Для компактности $ (0,1) $. Каждая открытая крышка имеет конечное дополнительное покрытие. Только одна открытая крышка. Есть и другие, и если $ (0,1) $ не компактно, по крайней мере одна открытая крышка не будет иметь открытой крышки.Но если каждые возможных открытых крышек, любые открытых крышек, о которых может подумать любой во вселенной, имеют конечное подпокрытие, тогда $ (0,1) $ компактно. Предположим, я сказал: Страна «богатая», если у каждого человека есть более 500 000 долларов. И я сказал: Америка не богата, потому что не у каждого человека есть более 500 000 долларов. И вы сказали: а что насчет Малькольма Форбса? У него более 500000 долларов. Так разве Америка не «богатая» страна. Ответ на этот вопрос — Малкольм Форбс — не каждый человек.Чтобы быть «богатым» , каждый должен иметь более 500 000 долларов. Итак, вопрос сводится к следующему: можем ли мы представить себе открытое покрытие $ (0,1) $, которое не имеет конечного подпокрытия? В комментарии Сантана Афтон привела хороший пример открытого покрытия в $ (0,1) $, которое не имеет конечного дополнительного покрытия. |