Покрытие множества — Википедия
У этого термина существуют и другие значения, см. Покрытие.Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊆⋃α∈AUα.{\displaystyle X\subseteq \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊆T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subseteq {\mathcal {T}}} называется
- Y⊆⋃α∈AUα.{\displaystyle Y\subseteq \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Если C{\displaystyle C} — покрытие множества Y{\displaystyle Y}, то любое подмножество D⊆C{\displaystyle D\subseteq C}, также являющееся покрытием Y{\displaystyle Y}, называется подпокры́тием.
- Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие впи́сано во второе. Более точно, покрытие D={Vβ}β∈B{\displaystyle D=\{V_{\beta }\}_{\beta \in B}} вписано в покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}}, если
- ∀β∈B∃α∈A{\displaystyle \forall \beta \in B\;\exists \alpha \in A} такое, что Vβ⊆Uα.{\displaystyle V_{\beta }\subseteq U_{\alpha }.}
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется лока́льно коне́чным, если для каждой точки y∈Y{\displaystyle y\in Y} существует окрестность U∋y{\displaystyle U\ni y}, пересекающаяся лишь с конечным числом элементов C{\displaystyle C}, то есть множество {α∈A∣Uα∩U≠∅}{\displaystyle \{\alpha \in A\mid U_{\alpha }\cap U\not =\varnothing \}} конечно.
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется фундамента́льным, если всякое множество, пересечение которого с каждым множеством U∈C{\displaystyle U\in C} открыто в U{\displaystyle U}, открыто и в Y{\displaystyle Y}.
- Y{\displaystyle Y} называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y{\displaystyle Y} называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
- Карта (математика)
- Нерв покрытия
- Размерность Лебега
- ↑ Покрытие множества — статья из Математической энциклопедии. А. В. Архангельский, П. С. Солтан
Открытое покрытие — это… Что такое Открытое покрытие?
- Открытое покрытие
Покры́тие в математике — это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии.
Определения
- Пусть дано множество X. Семейство множеств

Связанные определения
- Если C — покрытие множества Y, то любое подмножество
 , также являющееся покрытием Y, называется
, также являющееся покрытием Y, называется - Если каждый элемент одного покрытия является подмножеством какого либо элемента второго покрытия, то говорят, что первое покрытия впи́сано во второе. Более точно, покрытие
 вписано в покрытие
вписано в покрытие  , если
, если
 такое, что
такое, что 
- Покрытие
 множества Y называется лока́льно коне́чным, если для каждой точки
множества Y называется лока́льно коне́чным, если для каждой точки  существует окрестность
существует окрестность  , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество 
- Y называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
- Пусть дано множество X. Семейство множеств
Wikimedia Foundation. 2010.
- Открытое отображение
- Открытое подмножество
Смотреть что такое «Открытое покрытие» в других словарях:
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (математика) — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (в геометрии)
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X. 1) Под П. топологического пространства, равномерного пространства и вообще какого либо множества, наделенного тем или иным строением, понимают произвольное П.… … Математическая энциклопедия
Локально конечное покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
ЛОКАЛЬНО КОНЕЧНОЕ ПОКРЫТИЕ — покрытиетопологич. пространства его подмножествами такое, что у каждой точки есть окрестность, пересекающаяся лишь с конечным числом элементов этого покрытия. Не из всякого открытого покрытия прямой можно выделить Л. к. п.: достаточно рассмотреть … Математическая энциклопедия
ПАРАКОМПАКТНОСТИ КРИТЕРИИ — следующие утверждения, равносильные для произвольного вполне регулярного хаусдорфова пространства X.1) Xпаракомпактно. 2) В каждое открытое покрытие пространства Xможно вписать локально конечное открытое покрытие. 3) В каждое открытое покрытие… … Математическая энциклопедия
ПАРАКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в любое открытое покрытие к рого можно вписать локально конечное открытое покрытие. (Семейство g множеств, лежащих в топологич. пространстве X, наз. локально конечным в X, если у каждой точки существует окрестность в… … Математическая энциклопедия
Топология — (от греч. tоpos место и …логия (См. …Логия) часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных… … Большая советская энциклопедия
Покрытие множества — Википедия
У этого термина существуют и другие значения, см. Покрытие (значения).Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊂⋃α∈AUα.{\displaystyle X\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊂T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subset {\mathcal {T}}} называется открытым покрытием множества Y⊂X{\displaystyle Y\subset X}, если
- Y⊂⋃α∈AUα.{\displaystyle Y\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
Связанные определения
- Если C{\displaystyle C} — покрытие множества Y{\displaystyle Y}, то любое подмножество D⊂C{\displaystyle D\subset C}, также являющееся покрытием Y{\displaystyle Y}, называется подпокры́тием.
- Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие впи́сано во второе. Более точно, покрытие D={Vβ}β∈B{\displaystyle D=\{V_{\beta }\}_{\beta \in B}} вписано в покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}}, если
- ∀β∈B∃α∈A{\displaystyle \forall \beta \in B\;\exists \alpha \in A} такое, что Vβ⊂Uα.{\displaystyle V_{\beta }\subset U_{\alpha }.}
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется лока́льно коне́чным, если для каждой точки y∈Y{\displaystyle y\in Y} существует окрестность U∋y{\displaystyle U\ni y}, пересекающаяся лишь с конечным числом элементов C{\displaystyle C}, то есть множество {α∈A∣Uα∩U≠∅}{\displaystyle \{\alpha \in A\mid U_{\alpha }\cap U\not =\varnothing \}} конечно.
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется фундамента́льным, если всякое множество, пересечение которого с каждым множеством U∈C{\displaystyle U\in C} открыто в Y{\displaystyle Y}, само открыто.
- Y{\displaystyle Y} называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y{\displaystyle Y} называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
- Карта (математика)
- Нерв покрытия
- Размерность Лебега
Примечания
- ↑ Покрытие множества — статья из Математической энциклопедии. А. В. Архангельский, П. С. Солтан
Покрытие множества — Карта знаний
- Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств.
В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами.
Источник: Википедия
Связанные понятия
Задача о покрытии множества является классическим вопросом информатики и теории сложности. Данная задача обобщает NP-полную задачу о вершинном покрытии (и потому является NP-сложной). Несмотря на то, что задача о вершинном покрытии сходна с данной, подход, использованный в приближённом алгоритме, здесь не работает. Вместо этого мы рассмотрим жадный алгоритм. Даваемое им решение будет хуже оптимального в логарифмическое число раз. С ростом размера задачи качество решения ухудшается, но всё же довольно… Откры́тое мно́жество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью (в метрических пространствах и, в частности, на числовой прямой). Например, внутренность шара (без границы) является открытым множеством, а шар вместе с границей — не является открытым. В теории графов доминирующее множество для графа G = (V, E) — это подмножество D множества вершин V, такое, что любая вершина не из D смежна хотя бы одному элементу из D. Число доминирования γ(G) — это число вершин в минимальном доминирующем множестве G. В математике конечное правило подразделения — это рекурсивный способ деления многоугольника и других двумерных фигур на всё меньшие и меньшие части. Правила подразделения в этом смысле является обобщением фракталов. Вместо повторения одного и того же узора снова и снова здесь имеются небольшие изменения на каждом шаге, что позволяет получить более богатые структуры, сохраняя при этом поддержку элегантного стиля фракталов . Правила подразделения используются в архитектуре, биологии и информатике… Конфигурация — это разбиение d-мерного линейного, аффинного или проективного пространства на связные открытые ячейки, порождённые конечным набором геометрических объектов. Иногда эти объекты имеют один и тот же тип, такой как гиперплоскости или сферы. Интерес к изучению конфигураций вызван успехами в вычислительной геометрии, где конфигурации были объединяющими структурами для многих задач. Успехи в изучении более сложных объектов, таких как алгебраические поверхности, отвечали нуждам приложений… Размерность Вапника — Червоненкиса или VC-размерность — это характеристика семейства алгоритмов для решения задачи классификации с двумя классами, характеризующая сложность или ёмкость этого семейства. Это одно из ключевых понятий в теории Вапника-Червоненкиса о статистическом машинном обучении, названное в честь Владимира Вапника и Алексея Червоненкиса. Аддитивная комбинаторика (от англ. addition — сложение) — междисциплинарная область математики, изучающая взаимозависимость различных количественных интерпретаций понятия структурированности подмножества группы (как правило, конечной), а также аналогичные свойства производных от множества структур, использующихся при этих интерпретациях. Кроме того, аддитивная комбинаторика изучает структурированность в различных смыслах некоторых специфических множеств или классов множеств (например, подмножеств… Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.Подробнее: Фундаментальная область
Произведение топологических пространств — это топологическое пространство, полученное, как множество, декартовым произведением исходных топологических пространств, и снабжённое естественной топологией, называемой топологией произведения или тихоновской топологией. Слово «естественная» здесь употребляется в смысле теории категорий и означает, что эта топология удовлетворяет некоторому универсальному свойству. Программа минимальных моделей — это часть бирациональной классификации алгебраических многообразий. Её цель — построение как можно более простой бирациональной модели любого комплексного проективного многообразия. Предмет основывается на классической бирациональной геометрии поверхностей, изучаемой итальянской школой и в настоящее время находящейся в активном изучении. Теория комбинаторных схем — это часть комбинаторики (раздела математики), рассматривающая существование, построение и свойства семейств конечных множеств, структура которых удовлетворяет обобщённым концепциям равновесия и/или симметрии. Эти концепции не определены точно, так что объекты широкого диапазона могут пониматься как комбинаторные схемы. Так, в одном случае комбинаторные схемы могут представлять собой пересечения множеств чисел, как в блок-схемах, а в другом случае могут отражать расположение…Подробнее: Комбинаторная схема
В теории графов и комбинаторной оптимизации двудольная размерность или число бикликового покрытия графа G = (V, E) — это минимальное число биклик (то есть полных двудольных подграфов), необходимых, чтобы покрыть всё рёбра E. Набор биклик, покрывающих все рёбра в G, называется бикликовым покрытием рёбер, или просто бикликовым покрытием. Двудольная размерность графа G часто обозначается символом d(G).Подробнее: Двудольная размерность
В геометрии подстановки плиток — это метод построения мозаик. Наиболее важно, что некоторые подстановки плиток образуют апериодические мозаики, то есть замощения, протоплитки которых не образуют какую-либо мозаику с параллельным переносом. Наиболее известные из них — мозаики Пенроуза. Подстановочные мозаики являются специальными случаями правил конечного подразделения, когда не требуется геометрическое равенство плиток. Мно́жество — одно из ключевых понятий математики; это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством. Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики. В общей топологии локальная конечность является свойством семейства подмножеств топологического пространства. Это понятие является естественным обобщением понятия конечного семейства и играет ключевую роль при изучении паракомпактности и топологической размерности.Подробнее: Локально конечное семейство подмножеств
А́лгебра (от араб. الْجَبْر, «аль-джабр» — восполнение) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множеств произвольной природы, обобщающий обычные операции сложения и умножения чисел. Выпуклая геометрия — ветвь геометрии, изучающая выпуклые множества, в основном, в евклидовом пространстве. Выпуклые множества возникают естественным образом во многих областях, в том числе в вычислительной геометрии, выпуклом анализе, комбинаторной геометрии, функциональном анализе, геометрии чисел, интегральной геометрии, линейном программировании, теории вероятностей. Синглетон — множество с единственным элементом. Например, множество {0} является синглетоном. В геометрии домино замощение области в евклидовой плоскости — это мозаика области плитками домино, образованными объединением двух единичных квадратов, соединённых по ребру. Эквивалентно это паросочетание в графе решётки, образованное помещением вершины в центр каждого квадрата области и соединением двух вершин, если два соответствующих квадрата смежны. Алгебраическая комбинаторика — это область математики, использующая методы общей алгебры, в особенности теории групп и теории представлений, в различных комбинаторных контекстах и, наоборот, применяющая комбинаторные техники к задачам в алгебре. Сравнение топологий — это понятие, позволяющее «сравнивать» различные топологические структуры на одном и том же множестве. Множество всех топологий на фиксированном множестве образует частично упорядоченное множество относительно этого отношения. Гру́ппа в математике — множество, на котором определена ассоциативная бинарная операция, причём для этой операции имеется нейтральный элемент (аналог единицы для умножения), и каждый элемент множества имеет обратный. Ветвь общей алгебры, занимающаяся группами, называется теорией групп. Алгебраическая поверхность — это алгебраическое многообразие размерности два. В случае геометрии над полем комплексных чисел алгебраическая поверхность имеет комплексную размерность два (как комплексное многообразие, если оно неособо), а потому имеет размерность четыре как гладкое многообразие. Суперквадрики — семейство геометрических поверхностей, определяемых уравнением эллипсоида и других поверхностей второго порядка, где показатели степени 2 заменены произвольным числом. Их можно считать трёхмерными аналогами кривых Ламе (суперэллипсов). Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических… В проективной геометрии конфигурация на плоскости состоит из конечного множества точек и конечной конфигурации прямых, таких, что каждая точка инцидентна одному и тому же числу прямых и каждая прямая инцидентна одному и тому же числу точек. Теорема Сарда — одна из теорем математического анализа, имеющих важные приложения в теории катастроф и теории динамических систем.Названа в честь американского математика Артура Сарда. Универсальное множество точек порядка n — это множество S точек евклидовой плоскости со свойством, что любой планарный граф с n вершинами имеет рисунок с прямыми рёбрами, в котором все вершины располагаются в точках множества S. Теорема об уголках — доказанный результат в области аддитивной комбинаторики, утверждающий присутствие некой упорядоченной (в арифметическом смысле) структуры, называемой уголком, в достаточно больших двумерных множествах любой фиксированной плотности. Теория Рамсея — раздел математики, изучающий условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. Названа в честь Фрэнка Рамсея. Бордизм, также бордантность — термин топологии, употребляющийся самостоятельно или в составе стандартных… Задача о вершинном покрытии — NP-полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP-полноты более сложных задач. Факторизация целых чисел для больших чисел является задачей большой сложности. Не существует никакого известного способа, чтобы решить эту задачу быстро. Её сложность лежит в основе некоторых алгоритмов шифрования с открытым ключом, таких как RSA. В геометрии гипотеза Келлера — это высказанная Отт-Генрихом Келлером гипотеза о том, что в любой мозаике в евклидовом пространстве, состоящей из однинаковых гиперкубов, найдутся два куба, соприкасающиеся грань-к-грани. Например, как показано на рисунке, в любой мозаике на плоскости из одинаковых квадратов, какие-то два квадрата должны соприкасаться ребро-к-ребру. Перрон доказал, что это верно в размерностях до 6. Однако для больших размерностей это неверно, как показали Лагарис и Шор для размерностей… Плитки Вана (или домино Вана), впервые предложенные математиком, логиком и философом Хао Ваном в 1961, — это класс формальных систем. Они моделируются визуально с помощью квадратных плиток с раскрашиванием каждой стороны. Определяется набор таких плиток (например, как на иллюстрации), затем копии этих плиток прикладываются друг к другу с условием согласования цветов сторон, но без вращения или симметрического отражения плиток. Задача со счастливым концом — утверждение о том, что любое множество из пяти точек на плоскости в общем положении имеет подмножество из четырёх точек, которые являются вершинами выпуклого четырёхугольника. Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств. Нерв покрытия — конструкция в топологии, дающая симплициальный комплекс по произвольному покрытию. Конфигурация прямых (или разбиение плоскости прямыми) — это разбиение плоскости, образованное набором прямых. В математике константой Чигера (также числом Чигера или изопериметрическим числом) графа называется числовая характеристика графа, отражающая, есть ли у графа «узкое место» или нет. Константа Чигера как способ измерения наличия «узкого места» представляет интерес во многих областях, например, для создания сильно связанных компьютерных сетей, для тасования карт и в топологии малых размерностей (в частности, при изучении гиперболических 3-мерных многообразий). Названа в честь математика Джефа Чигера… Симплициальное множество (в ранних источниках — полусимплициальный компле́кс) — теоретико-категорная конструкция, обобщающая понятие симплициального комплекса и в определённом смысле моделирующая понятие топологического пространства с «хорошими» свойствами: теория гомотопий для симплициальных множеств эквивалентна классической теории гомотопий для топологических пространств. За счёт того, что является чисто алгебраической конструкцией, обеспечивает практически полный параллелизм с геометрическими… Теория групп — раздел общей алгебры, изучающий алгебраические структуры, называемые группами, и их свойства. Группа является центральным понятием в общей алгебре, так как многие важные алгебраические структуры, такие как кольца, поля, векторные пространства, являются группами с расширенным набором операций и аксиом. Группы возникают во всех областях математики, и методы теории групп оказывают сильное влияние на многие разделы алгебры. В процессе развития теории групп построен мощный инструментарий… Общая топология, или теоретико-множественная топология, — раздел топологии, в котором изучаются понятия «непрерывности» и «предела» в наиболее общем смысле. Теорема Курселя — утверждение о том, что любое свойство графа, определяемое в логике графов второго порядка, может быть установлено за линейное время на графах с ограниченной древесной шириной. Результат впервые доказан Брюно Курселем в 1990 году и независимо переоткрыт Бори, Паркером и Товейем. Род многообразия — гомоморфизм кольца кобордизмов замкнутых многообразий в некоторое кольцо, обычно кольцо рациональных чисел. В математике термин матрица Картана имеет три значения. Все они названы по имени французского математика Эли Картана. Фактически, матрицы Картана в контексте алгебр Ли впервые исследовал Вильгельм Киллинг, в то время как форма Киллинга принадлежит Картану.Подпокрытие — это… Что такое Подпокрытие?
Лемма Гейне — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Лемма Гейне — Бореля — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Теорема Александера о предбазе — Теорема Александера о предбазе[1] (англ. Alexander Subbase Theorem) теорема общей топологии, устанавливающая критерий компактности топологического пространства. Компактным называется пространство, допускающая выделение из каждого своего… … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X. 1) Под П. топологического пространства, равномерного пространства и вообще какого либо множества, наделенного тем или иным строением, понимают произвольное П.… … Математическая энциклопедия
Глоссарий общей топологии — Эта страница глоссарий. См. также основную статью: Общая топология В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глос … Википедия
БИКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в каждом открытом покрытии к рого содержится конечное подпокрытие того же пространства. Следующие утверждения равносильны: 1) пространство Xбикомпактно; 2) пересечение любой центрированной системы замкнутых в… … Математическая энциклопедия
БОРЕЛЯ — ЛЕБЕГА ТЕОРЕМА — о покрытии: пусть А ограниченнее замкнутое множество в Rn и G его открытое покрытие, т;, е: еистема открытых множеств, объединение к рых включает А; тогда существует конечная подсистема множеств , из G(подпокрытие), также являющаяся покрытием А … Математическая энциклопедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
Словарь терминов общей топологии — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч … Википедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (математика) — это… Что такое Покрытие (математика)?
Покрытие (значения) — Покрытие: Покрытие (математика) семейство множеств, объединение которых содержит данное множество. Покрытие (конструкция) верхняя конструкция здания Покрытие (материал) поверхностный слой, материал Критерий тестового покрытия метрика в… … Википедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (в геометрии) — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Локально конечное покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Открытое покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Карта (математика) — Содержание 1 Карта 2 Согласованные карты 3 Покрытие пространства 4 Атлас … Википедия
Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Схема (математика) — В алгебраической геометрии схема это абстракция, позволяющая связать единым образом коммутативную алгебру и дифференциальную геометрию и переносить идеи из одной области в другую. В первую очередь понятие схемы позволяет перенести… … Википедия
Задача о вершинном покрытии — NP полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP полноты более сложных задач. Содержание 1 Определение 2 NP полнота 3 Ссылки … Википедия
Александр II (часть 2, XIII-XIX) — XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия
Покрытие множества Википедия
У этого термина существуют и другие значения, см. Покрытие.Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения[ | ]
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊆⋃α∈AUα.{\displaystyle X\subseteq \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A
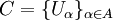
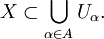
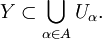
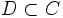 , также являющееся покрытием Y, называется
, также являющееся покрытием Y, называется 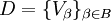 вписано в покрытие
вписано в покрытие 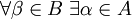 такое, что
такое, что 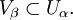
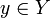 существует окрестность
существует окрестность 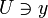 , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество